Why Can It Sometimes Be So Darn Difficult to Find Politicians Who Do What *Voters* Want?
More specifically, Public Choice Theory and the Political Principal-Agent Problem

Introduction
We have spent a lot of time in the past identifying reasons why governments might actually need to exist for the good of society and the economy, but this was not meant to imply government intervention is always a good thing. Thus, the purpose of this issue of Walls and Bridges is to demonstrate that despite justifications for government involvement in economic transactions, such intervention also has its drawbacks.
This is actually something we have written about elsewhere awhile back, but given the fact municipal elections will be held in Alberta on October 20, we thought it would be timely to cover it again now.
In short, politicians actually behave like real people who try to maximize their own welfare, even if it lowers the total welfare of the society they are supposed to represent.
This article will proceed in two main parts. First, we will cover public choice theory, which applies economic principles to understand economic decision making. These models assume individuals view government as a mechanism for maximizing welfare.
Thus, we will show that although direct democracy is nice in theory, it is highly infeasible because nothing will ever be accomplished. We will demonstrate this conclusion by studying two problems of direct democracy in the context of majority voting: the Voting Paradox and logrolling. We will then explain Arrow’s Impossibility Theorem, which tells us that no voting system can satisfy all conditions for a perfect system and still avoid the Voting Paradox.
Given problems with making direct democracy work effectively, representative democracies exist in the real world. However, we will explain problems associated with direct democracy still exist with representative democracies; moreover, new problems are created in these democracies such as the Political Principal-Agent Problem: it exists when principals — taxpayers and voters — cannot ensure their agents — political decision makers — will act in the best interest of the principals. Thus, we will learn how special interest groups can form to deal with this Principal-Agent Problem, and why these groups might do more harm than good.1
But before we begin, we want to point any Calgarians out there to Elections Calgary’s site here, which not only identifies all the candidates for political office in Calgary, but also their contact info and websites.
If you are in Edmonton, then go here for that information. Information for Red Deer is here, Lethbridge here, Medicine Hat here, and the Regional Municipality of Wood Buffalo (Fort McMurray) here.
If you are not in one of those municipalities, then you can search online for your area’s information by typing “elections” followed by your municipality’s name.
And now on to the show.
Public Choice Theory
The Voting Paradox
Unanimity in voting would be nice, but it is unlikely to happen in practice because:
It requires everyone to pay Lindahl prices, meaning every person pays exactly what they are willing to pay. But it also means if one can reasonably guess the other person’s marginal benefit, then they will try to act strategically to get that person to pay the real higher cost.
It can take a long time to run the auction enough times to get everyone to agree on the optimal quantity of the public good.
Typically, people only demand unanimity when they do not want a decision to be made, because they know their decision will not win if it is up for majority rule.
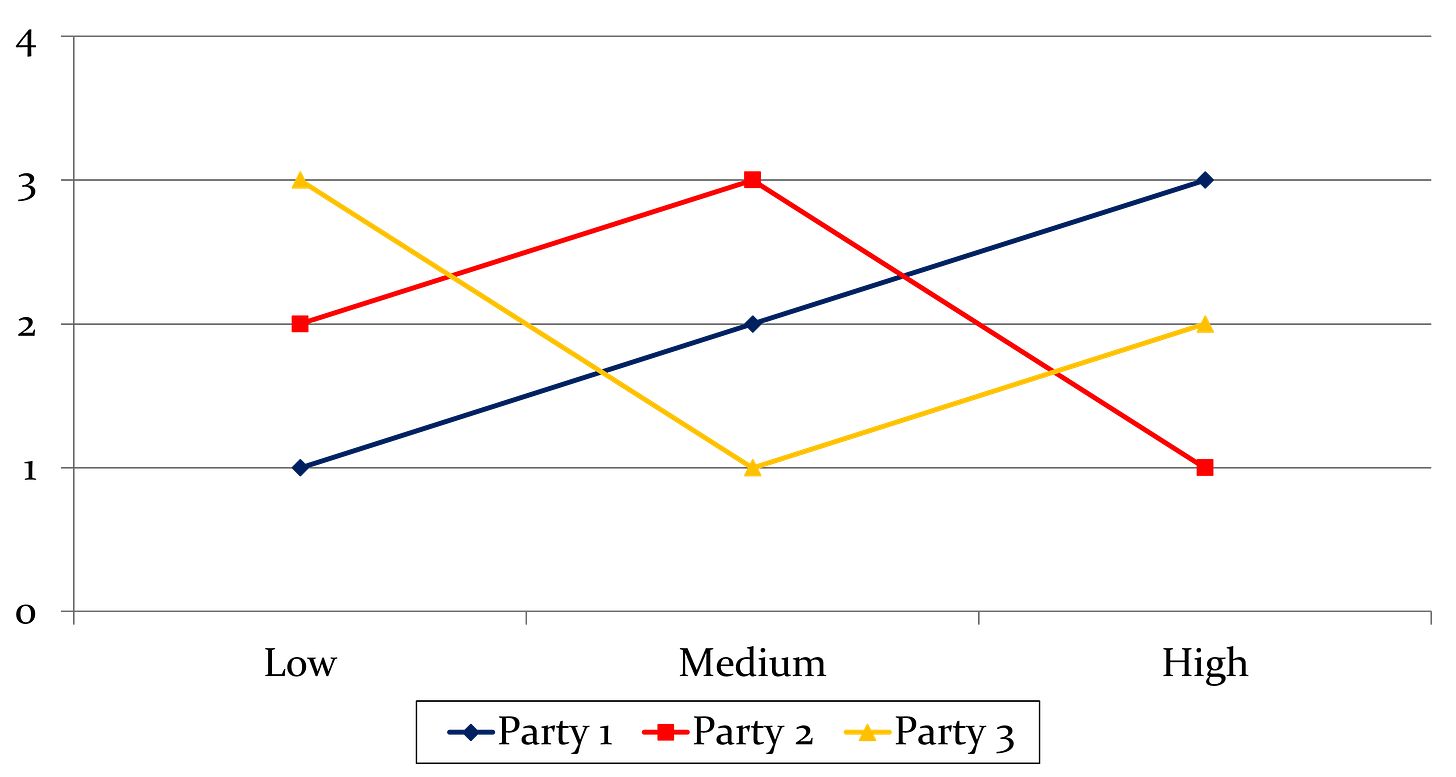
For an application of majority voting, consider three parties — Party 1, Party 2, Party 3 — who use majority rule to decide spending on high-speed rail. There are three options for spending: High (H), Medium (M), and Low (L), and each individual ranks the options as shown in Table 1 below.
Consider all possible pair-wise elections: M versus H, H versus L, and L versus M. What is the outcome of each election? Does it appear majority rule will lead to a stable outcome on spending on defense? If so, what is the choice? Would giving one person the ability to set the agenda affect the outcome?
To answer these questions, there are three pairwise votes:
L vs. M: M wins 2 to 1 because Parties 2 and 3 prefer M to L
M vs. H: M wins 2 to 1 because Parties 1 and 2 prefer M to H
L vs. H: L wins 2 to 1 because Parties 1 and 2 prefer L to H
Thus, majority rule leads to a stable outcome (M, which is called the Condorcet winner) because the order in which they vote does not matter; it always wins in the end, even if we give one person the right to set the agenda.
Specifically:
If we begin with L vs. M, then M wins; in the runoff between M and H, M wins
If we begin with M vs. H, then M wins; in the runoff between M and L, M wins
If we begin with L vs. H, L wins; in the runoff between L and M, M wins
However, there are also problems inherent in a system of majority rule, as we will show next.
Suppose Party 1’s preference ordering changes to the following: first choice = L, second choice = H and third choice = M — so “all-or-nothing” preference ordering because this party believes a half-assed strategy will not work, so if they do not get their way then they will take their ball and go home.
The new set of preferences are in Table 2 below.
Would majority rule lead to a stable outcome? If so, what is the choice? Would giving one person the ability to control the agenda affect the outcome?
Again, we answer these questions by analyzing all three pairwise votes:
L vs. M: M wins 2 to 1 because Parties 2 and 3 prefer M to L
M vs. H: H wins 2 to 1 because Parties 1 and 3 prefer H to M
L vs. H: L wins 2 to 1 because Parties 1 and 2 prefer L to H
Therefore, the order in which they vote does matter now because:
If we begin with L vs. M, then M wins; in the runoff between M and H, H wins
If we begin with M vs. H, then H wins; in the runoff between H and L, L wins
If we begin with L vs. H, L wins; in the runoff between L and M, M wins
So a Voting Paradox exists where the final outcome of a vote between alternatives will differ depending on which two options are part of the first pairwise-vote.
This paradox arises if at least one voter has double-peaked preferences: their utility falls and then rises again as they move away from their preferred option. But keep in mind these preferences are only a necessary (not a sufficient) condition for the voting paradox to exist.
We can visualize double-peaked preferences as shown in Figure 1 below — not related to the previous examples — where this time Party 3 basically has an “all-or-nothing” preference ordering because if they cannot get their most preferred option (“Low”) then they will instead fight for the extreme opposite (“High”). Therefore, contrary to the other two players whose preference ordering peaks only once as we move from left to right, Party 3 has two peaks: “Low” and “High”.
Personally, we recognize the preferences of some U.S. voters as being double-peaked, specifically people who argued that if they could not have Bernie Sanders as POTUS, then they would prefer to have Donald Trump win the election instead of the more moderate Democrat running for office.
On the other hand, this paradox will never arise when all voters have single-peaked preferences: no matter which direction they move from their most-preferred outcome, they will always be worse off.
Single-peaked preferences are more unlikely when we are comparing very different options — for example, bookstore vs. abortion clinic vs. armed forces recruitment office — instead of different levels of funding for the same policy program.
The Voting Paradox can lead to cycling since a coalition of any two blocs of voters can defeat any motion. For example, in 1989 Canadian Prime Minister Brian Mulroney tried to legislate a compromised change to Canada’s abortion law with Bill C-43 — specifically, that abortions are legal, but only if the pregnancy threatened the life or health of the pregnant woman in question. Moreover, “health” was defined broadly to mean “physical, mental, and psychological health.”2
The problem was members on opposite ends of the abortion debate kept creating coalitions to strike any compromise down. Specifically, both pro-life and pro-choice camps would propose changes in committee that were so extreme that members in the middle ground would never accept it.
In other words, both moderates and pro-choice members would vote down any pro-life proposals; and both moderates and pro-life members would vote down any pro-choice proposals. Thus, no change was made to the law despite majorities in both the House and the Senate being very much against sticking with the status quo.
Median Voter Theorem
Which voter(s) will be most satisfied with the outcome of a vote when we do have single-peaked preferences?
The Median Voter Theorem tells us that as long as all preferences are single peaked, the majority voting outcome reflects the preferences of the median voter. With an even number of voters there are two median voters, so the tie is broken arbitrarily.
We can demonstrate this theorem using Table 3 below where we assume there are five people — Peter, Mark, Jag, Yves, and Liz — who are voting on how much to spend on an environmental-protection program. For example, Peter prefers to spend $50 while Liz prefers to spend $200.
As we can see, as the amount rises from zero everyone initially approves of the expenditure, but as soon as we move above $160 then a majority will vote against the expenditure. Therefore, the amount spent on the program will be exactly $160, which means the median voter is satisfied.
If the requirements for the median voter rule are satisfied in a direct vote over the quantity of a good, will the expenditure level most preferred by the median voter actually be efficient?
Not if the median voter does not pay their full marginal benefit of the program. Specifically, if they pay a less-than-equal share of the cost of the good, then they will likely vote for a level of expenditure higher than they would be willing to pay themselves, and therefore too much will be spent on the program.
Logrolling
Another problem with majority voting is it does not allow people to register how much they prefer an option. Thus, logrolling schemes can develop under majority voting which allow people to trade votes, and thus register how strongly they feel about certain issues.
Examples of logrolling include:
Strategic voting where I vote for your favourite party in my riding, if you vote for my favourite party in your riding.
A coalition —either formally or informally — such as the coalition between the Liberal Party and NDP in Ontario in 1985 that secured Premier David Peterson’s provincial government, or the agreements between the NDP and Green Party in British Columbia in 2017 and 2024 — not to mention the supply and confidence agreement between the federal Liberal Party and NDP in recent years.
Logrolling is a way for special interests to get their way through mutual back-scratching: if majority voting does not lead to the socially-optimal outcome, then special interests can demand politicians to add their policies — or some of them — to a bill before voting for it. So in effect, they agree to vote for each other’s policy by putting both in one bill.
As we will show next, while logrolling sometimes can improve overall welfare in society, it can also reduce it. See Table 4 below, where Peter, Paul, and Mary are voting on funding for a hospital, a library, and regional transit. Each number represents each person’s marginal benefit from each policy, so a negative number means they feel worse for having it.
Will logrolling improve welfare given the above marginal benefits?
First, the net benefit for all three options is positive — 95 for Hospital, 80 for Library, and 220 for Regional Transit — so all three options should be funded, but if there is a majority vote on each project one at a time, then none of them will be funded because two people will always vote against it.
Thus, different logrolling initiatives can lead to two policies being passed, such as Peter agreeing to regional transit in exchange for Mary agreeing to a hospital, as each person’s total benefit for the two policies is positive: 80 for Peter and 345 for Mary.
Mary could then agree to a library if Paul agrees to regional transit and also compensates her for the 30 she loses — since she has already made a deal with Peter so regional transit is safe. Paul will agree to this tradeoff because his total benefit after compensation is still 10.
So there are various ways all three programs can be funded as long as they can get together and negotiate.
Now suppose we change the numbers as in Table 5 below:
Now will logrolling improve welfare?
First, the net benefit for all three options is negative — -15 for Hospital, -10 for Library, and -10 for Regional Transit — so we should fund none of the programs, and majority rule will support this result.
But then we get problem of special interests: Peter and Paul can agree to both vote on both the hospital and library so they pass because the total benefit for Peter will be 160 and the total benefit for Paul will be 30.
In this case, we also see that the minority voter (Mary) pays most of the program costs for the majority since she is worse off with both programs. So in this circumstance, Mary is taking a big hit for Peter and Paul with no offsetting benefit to her. In other words, Regional Transit is not funded because the person who valued it (a lot) was excluded from the negotiation.
For a real-world application of logrolling, let’s take a look at omnibus bills, which can be used to pass a section of the bill that everyone wants, but then someone sneaks in something that some members really hate. As long as the other side has a positive total benefit across all policies in the omnibus bill, it will pass with minimal trouble.
For example, take North Carolina in the summer of 2013. During this time, there was a vote on an anti-Shariah law, but then Senators attached abortion restrictions to the same bill. The bill was passed 29-12.
Another example — also in North Carolina in the summer of 2013 — involved an abortion bill that was “tucked into motorcycle safety legislation” by House Republicans with no public notice, despite veto threats by the governor — but he apparently changed his mind. See here for more on it all.
To demonstrate how this worked, see the hypothetical numbers in Table 6 below.
Specifically, if each policy was up for votes separately, then only the motorcycle safety bill would pass because the net benefit across parties for it is 600, as opposed to the anti-abortion bill which is -50. But when voted together as one omnibus bill, then that bill passes because Democrats are less opposed to the anti-abortion bill than they like the motorcycle safety bill.
Very sneaky of the Republicans, but still legal.
Even in a majority government, politicians might perform this trick based on a long-run perspective: if the voter never finds out the “bad” part is in the omnibus bill — perhaps because the opposition had no time to really read the bill — then they cannot get mad enough to vote against the government.
Arrow’s Impossibility Theorem
We are now painfully aware it is very difficult to make direct democracy work in the real world. On the other hand, is there any ethically-acceptable method for translating individual preferences into collective preferences, and which does not face problems discussed above?
We could exhaustively compare and contrast each and every possible voting system, but doing so could take us decades. The following are just five of them:
Point voting: each voter is given a fixed number of points which are cast for the different alternatives.
Plurality voting: the alternative with the most votes wins, so one option can win with only 40% of the vote if there are more than two options (sound familiar?).
Borda counts: each alternative is ranked by each voter, and the ranks are totaled to choose the winner.
Condorcet elections: the alternative that defeats the rest in paired elections wins.
Exhaustive voting: the proposal favoured least by the largest number of voters is repeatedly removed until only one remains.
Regardless of which voting system is chosen, it is virtually — although not absolutely — impossible to find a perfect system. We can make such a strong statement because in 1951, Economics Nobel-laureate Kenneth Arrow proposed that in a democratic society, a collective decision-making rule should satisfy the following six criteria:
It can produce a decision regardless of how voter preferences are configured, so multi-peaked preferences cannot be a problem with this voting system.
It must be able to rank all possible outcomes.
It must be responsive to individual preferences: for example, if each individual prefers A to B, then so does society.
It must be consistent such that if A > B and B > C then A > C.
Independence of Irrelevant Alternatives: society’s ranking of A and B depends only on individual rankings of A and B, not on how A or B rank relative to C.
Dictatorship is ruled out.
Arrow then used some fairly sophisticated math to prove it is virtually impossible for all six conditions to hold simultaneously and still avoid the Voting Paradox: the Arrow Impossibility Theorem.
Representative Democracy
Our discussion so far assumed society should get what it wants, and the people responsible for carrying out society’s wishes are benevolent; we also assumed society’s opinions are solicited with constant referenda.
However, that is obviously not true — or really possible — in the real world. Instead, we elect politicians to decide what is best for us, and these people likely have their own selfish interests to consider.
In some respects, the Median Voter Theorem applies in a representative democracy because politicians will gravitate toward the centre to get as many votes as possible; that is indeed why they often propose very similar policies.
According to Downs (1957), the median voter will get its way as long as:
Preferences are single-peaked and cover the political spectrum
Voters want to maximize their own utility
Politicians seek to maximize the number of votes received
However, the median voter theorem can still fall apart due to:
No single-dimensional rankings: there exists no common median voter across all issues who stands waiting for politicians to pander to them and them alone. Thus, politicians will aim for a group of people large in numbers and relatively homogeneous — and potentially extreme — and pander to them instead.
Ideology: politicians might care more about ideological purity than about doing what most people want. In other words, they do not really want to win elections because that would require selling out to “The Man”. Instead, they exist to simply change minds of the electorate, and thus the people who do hold power.
Personality and leadership: voters often vote based on personalities so they might vote against a certain politician that has done a lot of good things for them, simply because they hate his (or her) guts. Similarly, they might vote for a total idiot simply because they would like to have a beer with him (sound familiar?).
Voter abstention: not everyone even votes, possibly because they believe their one vote will not make a difference in the grand scheme of things. Therefore, the politicians can ignore their needs and concentrate on those who actually vote.
There is one final problem with representative democracy that we will cover next, which is big: the Political Principal-Agent Problem.
The Political Principal-Agent Problem
Principal-Agent Problem
When we contract with people whose actions we cannot observe or evaluate, they might take advantage of us. We could monitor them to make sure they are doing their job properly, but this can be expensive or even impossible. Thus, we want to figure out how to make them monitor themselves, meaning they will not “shirk” their duties.
Politically, a Principal-Agent Problem exists when principals — taxpayers and voters — cannot ensure that agents — political decision makers — will act in the best interest of the principals. For example, many Ontario voters want Doug Ford to improve the healthcare system, but he instead spends time and money focusing on opposing bike lanes and building a tunnel under Highway 401, while offering $200 cheques and cheap beer to distract them from this foolishness.
You might have noticed this problem sounds an awful lot like the moral hazard problem. Well congratulations, because you are correct! Indeed, the Principal-Agent Problem arises because there is a moral hazard problem: governments tend to have more information than voters, so these governments shift the costs of their bad decisions to voters after the transaction (voting).
Thus, Adam Smith’s Invisible Hand does not necessarily apply to government choices. Even though governments should pursue the social objectives of efficiency and/or social equity, voters tend to have less information than politicians. Therefore, without checks and balances, politicians can use their special information to attract votes from special interest groups, which will be the subject of the next subsection.
If it is in the best interest of voters to obtain information, why don’t they obtain it?
Info is not readily available: for example, limited information provided in budget documents.
Rational ignorance: the marginal cost to an individual voter of obtaining information, or even of voting, is outweighed by their marginal benefit so they rely on special interest groups.
Free-rider problem: information is a public good so they wait for others (special interests) to find it.
This is why special interest groups — some good, some bad — arise.
Special Interest Groups
Even though individual voters theoretically have all of the power over politicians, special interest groups are often more powerful due to:
Group size and collective political action: special interest groups might be able to more easily coordinate their actions than millions of individual voters.
Money, money, money: special interests can finance ads to influence voters.
Salient policy issues: voters often focus on key issues, so the ones they ignore can be used by politicians to favour special interest groups.
Stakes in outcomes of political decisions: special interest groups put so much time and effort into a single issue or group of issues, that they fight harder to get their way than individual voters who have little stake in a single issue.
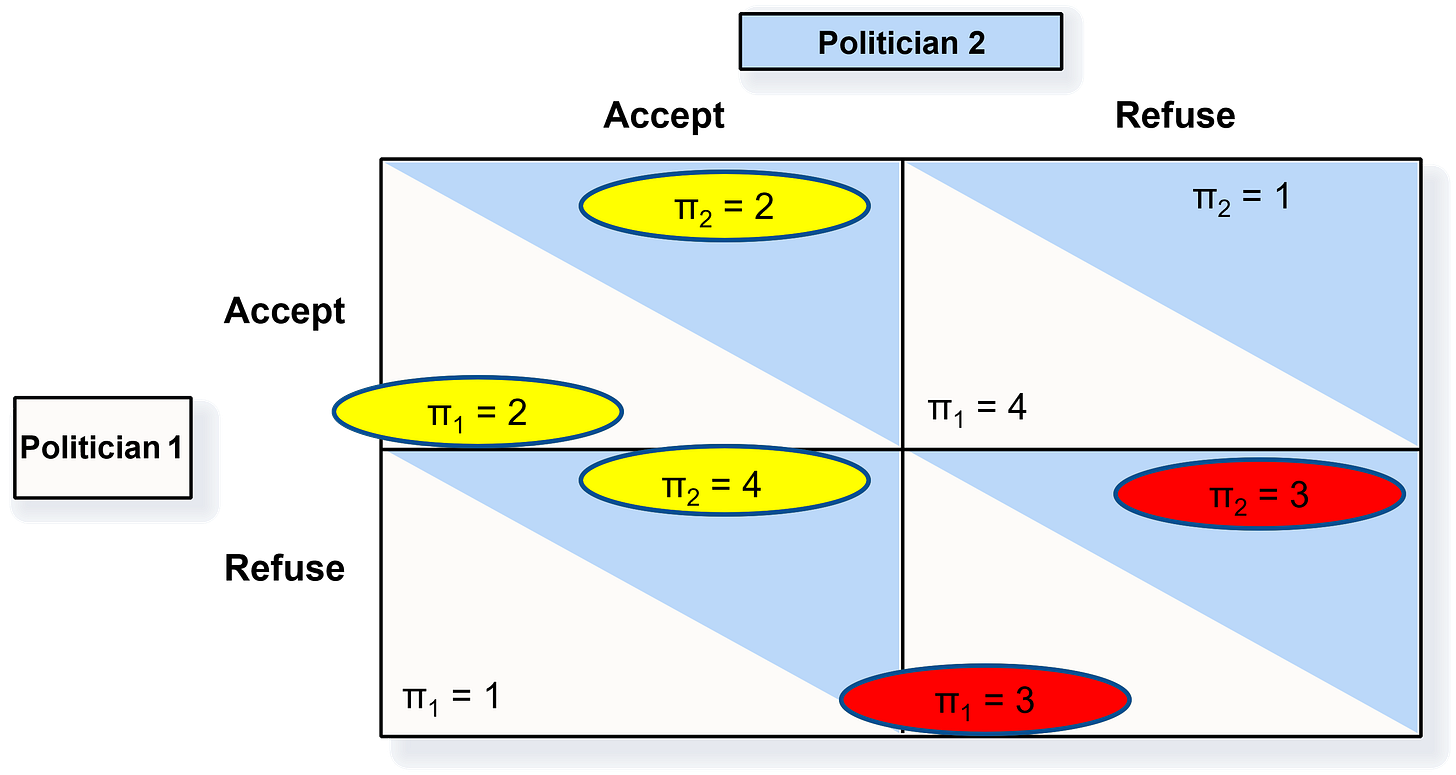
We will use game theory to demonstrate this problem. The game is summarized as follows, and shown in Figure 2 below:
Players: Politician 1 and Politician 2
Rules:
Each can choose to either Accept (A) campaign contributions from special interests or Refuse (R) them
They (essentially) make their choices simultaneously
Each player has complete, perfect, and symmetric information
Outcomes: (A, A), (A, R), (R, A), (R, R)
Payoffs: if both players accept contributions from special interests, then they will each make a payoff of 2. However, if one accepts these contributions and the other refuses them, then the accepter will raise their payoff to 4 by also taking contributions the other player refused, while the one refusing contributions will reduce their payoff to 1 — they still get a positive payoff because at least some regular voters will recognize their high morals and give contributions themselves. But if they both refuse special interest contributions, then they will each make a payoff of 3 — which is higher than if they both accepted these contributions because there is less voter cynicism, so regular voters will donate more to them.
To solve this game, we begin by assuming we are one of the two players. It does not matter which player we choose first, so suppose we are Politician 2 and we assume Politician 1 accepts special interest contributions. In that case, Politician 2 has a choice of accepting special interest contributions and making a payoff of 2, or refusing special interest contributions and earning a payoff of 1. Clearly, Politician 2 is rational so they want to accept special interest contributions. We then circle their payoff of π2 = 2 to represent a best response.
To properly solve the game, we must exhaust all possible moves that could be made by Politician 1. We already figured out Politician 2’s best response to Politician 1 accepting special interest contributions, so we must now determine his best response if Politician 1 refuses special interest contributions. In that case, Politician 2 can either accept special interest contributions and earn a payoff of 4 or refuse special interest contributions an earn a payoff of 3. Since Prisoner 2 is rational, they will choose to accept special interest contributions and maximize his payoff. Thus, we circle π2 = 4 to represent another best response.
We can now see that Politician 2 has a strictly dominant strategy: accept the special interest contributions. Since they will never choose to refuse them, we can safely ignore that strategy. Given complete, perfect and symmetric information, Politician 1 understands this strictly dominant strategy and will thus only have to decide whether or not to accept the contributions given Politician 2’s obvious preference for doing the same: if Politician 1 also accepts the contributions, they will earn a payoff of 2 instead of 1 if they refuse them. Being rational, they will obviously choose to accept special interest contributions so we circle π1 = 2 to represent a best response.
We have now exhausted all possible strategies, and we see there is only one cell in the table where both payoffs are circled — and highlighted in yellow — as best responses: (A, A). That cell is the unique solution of the game, as neither player can unilaterally improve their payoff by changing their strategy if they find themselves in this cell.
However, if they could enforce a binding agreement with one another to make this a cooperative game, then the politicians would choose to refuse the special interest contributions. Doing so would result in both players earning payoffs of 3, i.e., the payoffs circled in red.
The problem with reaching this jointly-optimal strategy lies in their inability to enforce the cooperative agreement, thus making it a Prisoner’s Dilemma: both players would be better off if they cooperated and chose different strategies, but neither one can trust the other to keep their end of the bargain due to the game rules!
How might this Prisoner’s Dilemma game be solved?
Caps on campaign contributions, particularly from unions and corporations: special interests can get around these rules with in-kind donations, such as time and non-monetary gifts — for example, celebrity endorsements. More money can also be given to parties/candidates by getting someone else to give it instead.
Limit campaign spending so the campaigner cannot spend their way into power: they can get around these rules in the U.S. with PACs, for example. Another drawback is that strict spending limits can hinder the chances of good politicians with little brand recognition.
Term limits: “lame duck” candidates are less likely to pander to special interests because can’t get reelected anyway. Drawbacks: the candidate might care about the future of their party’s successor. Also, limits can push out good politicians who actually know what they are doing, leaving us with inexperienced politicians.
Require majority to get power, so they will try to please as many different voters as possible to get into power. Drawbacks:
“Tyranny of the majority” where the majority passes policies to weaken the minority.
They might pander to a splinter party just to get a majority.
They could also gerrymander, which means they change election boundaries to ensure victory.
They might also be able to just pander to certain regions — such as Ontario and Quebec in Canadian federal elections — which have a majority of seats in the country.
Parties could be funded based on the number of seats they get, but that gives an advantage to the party with a majority when they go into next election.
A powerful, independent media with credibility and courage to call out governments for scandals. Drawbacks: media networks have become partisan themselves, such as Fox News and MSNBC.
Make the game a repeated one so they can be punished for bad behavior, but:
Powerful incumbent can motivate voters to ignore bad behavior.
Repeated interaction might make politicians more likely to cater to special interests because they do not want to be punished by those interests for backing out on them.
Repeated election cycle can discourage voters from caring about it all.
Publish campaign contributions to shame special interests. Drawbacks: could discourage average voter who just wants to give $10 to their favourite politician without being “seen” by employers, friends, family, etc.
Matching contributions whereby for every dollar collected from private citizens, another dollar will be given by the government so politicians will go away from special interests to double their money. Drawback: matching funds come from taxpayers, and evidence has shown it might make pander more to special interests because can please them without a money trail. Also opens people up to fudging numbers to make their private funding look bigger.
Here is another question: even though voters theoretically have the power, special interest groups are often more powerful. Why?
Group size and collective political action: special interest groups can more easily coordinate their actions than millions of voters.
Salient policy issues: voters focus on key issues, so the ones they ignore can be used to favour special interest groups.
Stakes in outcomes of political decisions: special interest groups put so much time and effort into a single issue or group of issues, they fight harder to get their way than individual voters who have little stake in a single issue.
Special interest groups can finance ads to influence voters
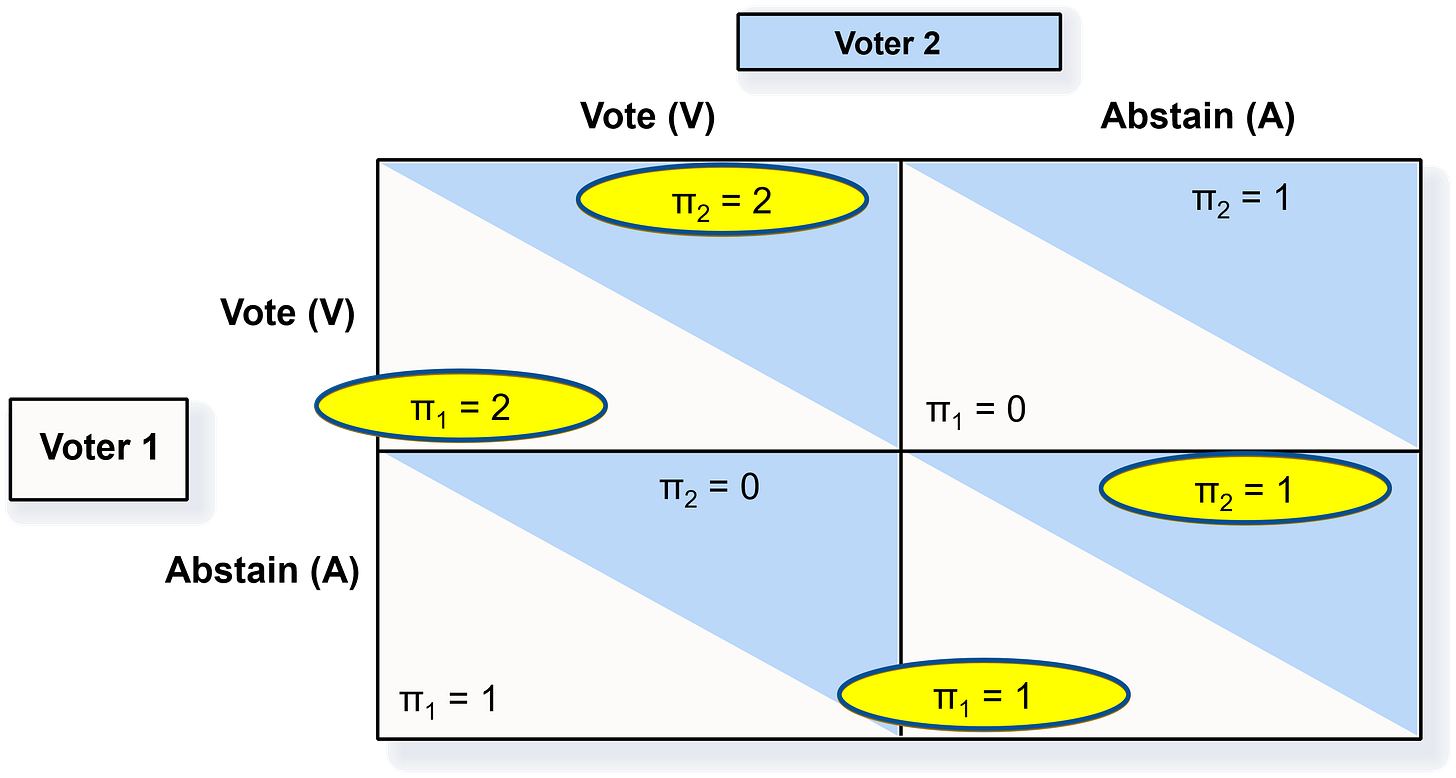
We will now use use game theory to analyze the problem of voter coordination. The game is summarized as follows, and shown in Figure 3 below:
Players: Voter 1 and Voter 2
Rules:
Each can choose to either Vote (V) or Abstain from Voting (A) them
They (essentially) make their choices simultaneously
Each player has complete, perfect, and symmetric information
Outcomes: (V, V), (V, A), (A, V), (A, A)
Payoffs: if both players vote, then they will each make a payoff of 2 because they got the result they wanted. However, if only one of them votes, then the voter will lower their payoff to 0 because they did not get the result they wanted and thus effectively “wasted their time”, while the abstainer will also reduce their payoff but only to 1 — they still get a positive payoff because they got to do something pleasurable instead of voting. But if they both abstain from voting, then they will each make a payoff of 1 because neither got what they wanted, but they got to do something pleasurable instead of voting.
We will leave it to you to solve this game step-by-step, but in the end there are two Nash Equilibria, because there are two cells both payoffs are highlighted in yellow as best responses: (V, V) and (A, A). Those cell are both solutions of the game because neither player can unilaterally improve their payoff by changing their strategy if they find themselves in one of these cells.
Therefore, they need to find some way to coordinate their strategies so they end up each getting the highest payoffs of 2. How might they do so without resorting to special interest groups?
Compulsory voting like in Australia and Greece. However, people in Australia have bragged publicly about getting drunk before voting, and not really thinking about how they voted. And Greece does not really enforce the law.
In countries where there is a cut-off date for registering to vote, allow people to register when they vote.
Change the electoral system — for example, from first-past-the-post to proportional — so people actually feel like their vote matters.
Change the system so more qualified people are motivated to run for office.
Rent Seeking
While special interest groups can be helpful to solve the voter-coordination problem, they also have drawbacks. One such drawback is rent seeking: they spend resources on maintaining market power or otherwise gaining special favours from politicians, when these resources could have otherwise been spent more productively. The greater the long-run gains from rent seeking, the more resources will be wasted.
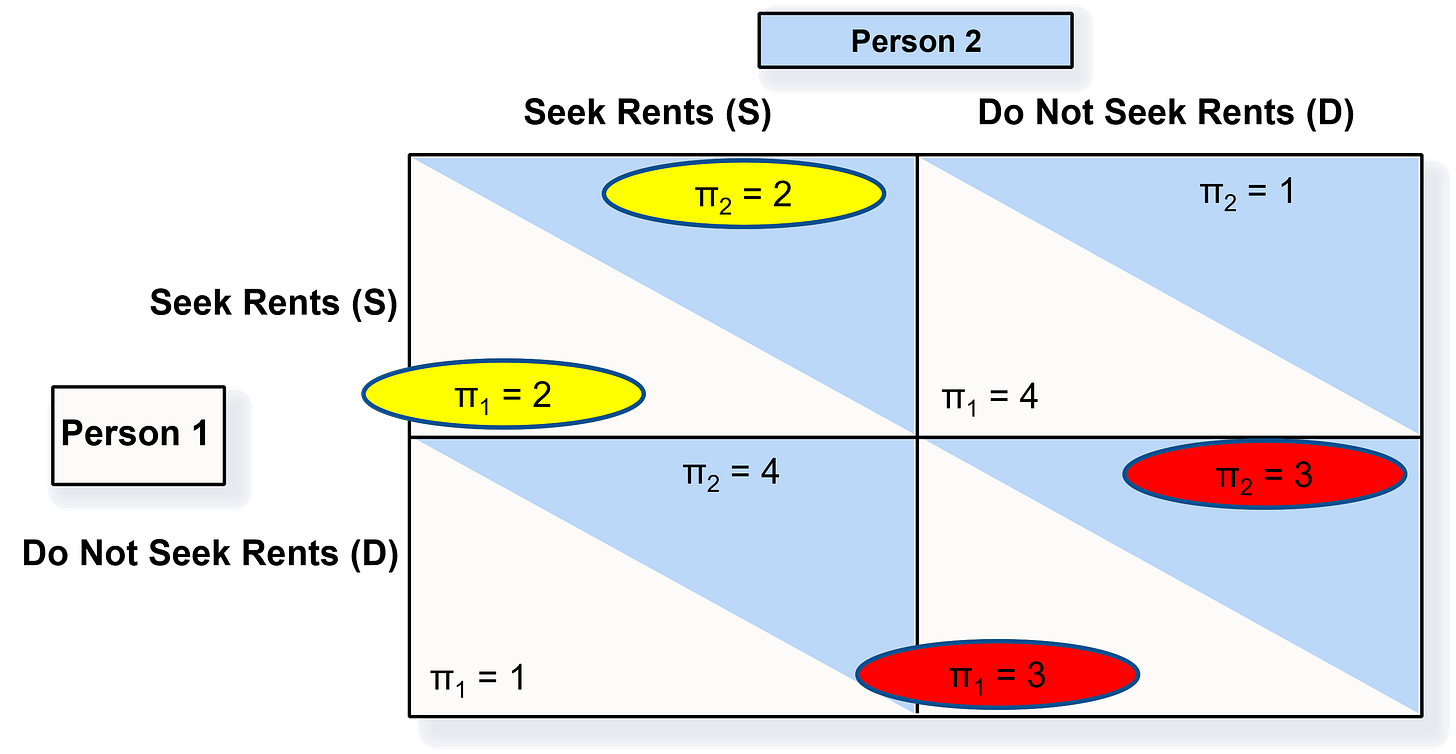
We will use use game theory to analyze the problem of rent-seeking. The game is summarized as follows, and shown in Figure 4 below:
Players: Person 1 and Person 2
Rules:
Each can choose to either Seek (S) rents or Do Not Seek (D) them
They (essentially) make their choices simultaneously
Each player has complete, perfect, and symmetric information
Outcomes: (S, S), (S, D), (D, S), (D, D)
Payoffs: if neither player seek rents, they will each make a payoff of 3 as they earn profits from competing with each other. However, if neither one seeks rents, then their payoffs will be reduced to 2 each because they still do not get special treatment, but they wasted resources trying to get it. Finally, if only one of them seeks rents, then the seeker will get special treatment and increase their payoff to 4, while the other one suffers for their morality and gets a reduced payoff of 1.
We will let you solve the game step-by-step yourselves, but in the end we see there is only one Nash Equilibrium in the game, which is where both players seek rents. This is also a Prisoner’s Dilemma because they would like to cooperate and not-seek rents, but they cannot trust the other one to be cooperative.
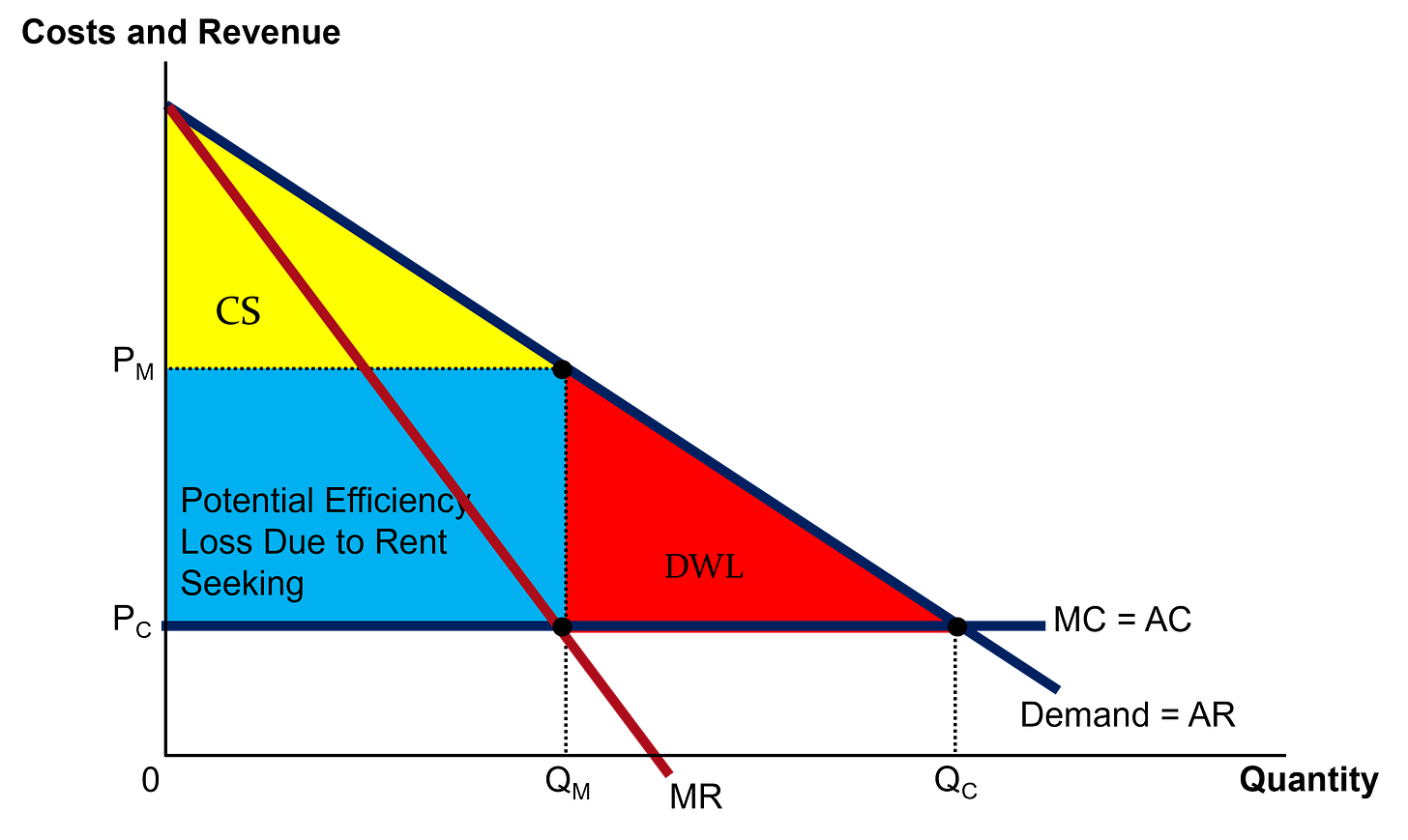
We can also demonstrate the effects of rent-seeking graphically in Figure 5 below.
In this graph, the social optimum — perfectly competitive ideal — is where price equals marginal cost, because that is where businesses make zero economic profits, so that is where price is PC and quantity sold is QC.
However, a profit-maximizing monopolist will set their price where their marginal revenue (MR) equals their marginal cost (MC) because that is where they make zero profits on the last unit sold — i.e., where the change in total revenue from increasing quantity marginally is equal to the change in total cost from increasing quantity by the same amount. This means the quantity sold is reduced to QM and the price charged is increased to PM.
The monopoly profit is then just the product of price and quantity, which gives the blue rectangle in the graph; consumer surplus is everything below the demand curve and above the price because the demand curve represents what they are willing to pay while the price is what they actually pay — so consumer surplus can be thought of as consumer profit.
By this logic, the monopolist lowers consumer surplus because in perfect competition, consumer surplus would be everything above PC and below the demand curve, which is all shaded areas combined.
Therefore, there is a deadweight loss (DWL) triangle created by the monopolist, which represents the loss in welfare to the entire economy because the monopolist charges too much for too little. This is the red triangle which would have gone to consumers under perfect competition, but goes to no one with a monopoly.
Now suppose the monopolist chooses to waste resources to either get that monopoly, or to keep it. For example, they might lobby the federal government to keep foreign competition out of the market so they face less competition. Then they would be willing to waste anything within the blue rectangle to maintain their monopoly power, which means —at least part of — that rectangle is also a loss to the economy.
How might rent-seeking be discouraged?
Clear and unimpeachable rules instead of discretion when handing out money or favours. In other words, trust will solve the Prisoner’s Dilemma game.
In general, raise the costs of lobbying, either in monetary terms or in reputation, such as publishing the names of donors.
Who else can affect government fiscal decisions? To be clear, their existence is not dependent on any particular issue, but they have influence nonetheless.
Bureaucrats: they can waste a lot of time and resources trying to convince people that they are more important than they really are.
Judiciary: for example, Canadian courts ruled the provincial sales tax is a direct tax so provinces can levy them, which is the opposite of the Australian experience where courts ruled it is an indirect tax. Also, the courts ruled in favour of equal same-sex benefits in Canada.
Journalists: for example, increased federal spending on AIDS research was partly motivated by increased media attention.
Experts can influence governments as much as special interests, perhaps more so in U.S.
International governments and organizations: for example, the World Bank and IMF. We might feel obligated to follow their policies.
Summary Remarks
In this article, we demonstrated there really is no perfect voting system. That is not surprising, but we now understand why systems such as majority voting are imperfect: a Voting Paradox can exist in which the order of the vote can affect the overall outcome; and special interests can use logrolling techniques that might reduce total welfare.
We also showed you all that while these problems can exist whether we are in a direct democracy or representative democracy; we also face a Political Principal-Agent Problem in the latter system. The reason for this problem is governments like to think they are also people, so they do bad things to further their own self interests.
And don’t get us started on how special interest groups only encourage such greedy behaviour!
Nonetheless, governments are still important so we need to understand these problems in order to minimize their negative implications, which is why we covered them: we cannot deal with a problem if we do not understand it.
Thank you for reading to the end. If you like what you see and want to support us with a paid subscription, then slam the “subscribe” button below! Regardless, we are glad you are here.
Of course, special interest groups might also exist specifically to tackle the Principal-Agent Problem, so special interest groups are not always bad for the economy.
Rosen, Harvey S., Jean-Francois Wen, and Tracy Snodden (2012). Public Finance in Canada, Fourth Canadian Edition. Toronto: McGraw-Hill Ryerson, page 109.